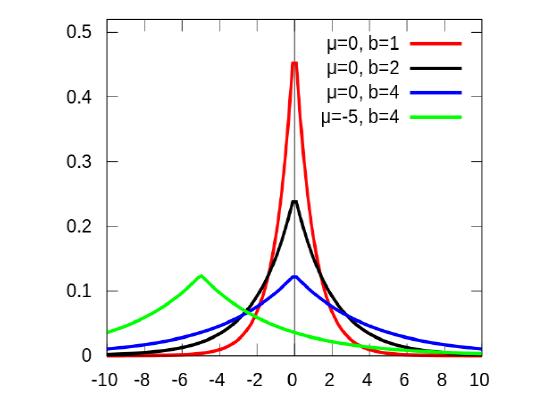
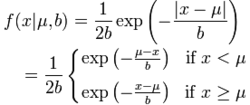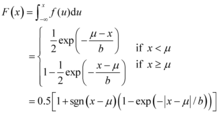如果随机变量的概率密度函数分布，那么它就是拉普拉斯分布，记为x-Laplace（μ,b），其中，μ是位置参数，b是尺度参数。如果μ=0，那么，正半部分恰好是尺度为1/b（或者b，看具体指数分布的尺度参数形式）的指数分布的一半。
精选百科
本文由作者推荐
拉普拉斯分布
1774年拉普拉斯提出的概念
中文名
拉普拉斯分布
外文名
The Laplace distribution
提出
拉普拉斯
领域
数学
性质
指数分布
发现时间
1774年
简介
如果随机变量的概率密度函数分布为
随机变量的概率密度函数分布
由拉普拉斯分布的概率密度函数联想到正态分布，但是，正态分布是用相对于μ平均值的差的平方来表示，而拉普拉斯概率密度用相对于平均值的差的绝对值来表示。因此，拉普拉斯分布的尾部比正态分布更加平坦。
累积分布函数
根据绝对值函数，如果将一个拉普拉斯分布分成两个对称的情形，那么很容易对拉普拉斯分布进行积分。
生成
已知区间（-1/2，1/2]中均匀分布上的随机变量U，随机变量为参数μ与b的拉普拉斯分布。根据上面的逆累计分布函数可以得到这样的结果。
当两个相互独立统分布指数（1/b）变化的时候也可以得到Laplace（0，b）变量。同样，当两个相互独立统分布一致变量的比值变化的时候也可以得到Laplace（0，1）变量。
相关研究
针对图像压缩感知重构问题，构建图像小波系数的广义拉普拉斯统计模型。首先通过对典型图像小波系数的直方图统计，以广义拉普拉斯分布拟合图像小波系数的先验概率密度，用KL散度法求得广义拉普拉斯分布的参数。然后基于贝叶斯准则，通过取对数，将稀疏系数的最大后验概率估计问题转化为p范数优化问题，其中p的取值由待重构的图像所决定，即为该图像小波系数对应的广义拉普拉斯分布的形状参数。最后由非凸优化法求解得到图像的小波系数，并实现图像的重构。[1]
实验结果表明：对于简单稀疏信号，该方法重构成功率明显高于经典的BP和OMP法；对于测试图像的小波系数信号，所提方法能够自适应地精确重构原始图像。
参考资料
1.基于广义拉普拉斯分布的图像压缩感知重构·知网空间
拉普拉斯分布 相关的文章
高奇，男，汉族，1962年3月生，山西临县人，大学学历。1982年12月参加工作，1987年12月加入中国共产党。2018年8月，经山西省纪委监委会议研究并报山西省委批准，决定给予高奇开除党籍、开除公职处分；将其涉嫌犯罪问题及所涉款物移送人民检察院依法审查、提起公诉.
王亮，残疾歌手，安徽阜阳界首市人，小时候因医疗事故致肌肉萎缩症。曾获2003年首届《中国少年儿童艺术节歌唱大赛》金奖，特别奖。2004年《中国星全国流行音乐大奖赛》青年组金奖。2005年《安徽残疾人音乐大奖赛》一等奖。著名歌唱家李谷一称赞他是少年天才歌手并致词鼓励捐助。
格林集团是伴随着中国现代市场经济发展而成长起来的民营企业。其前身格林期货经纪有限公司由集团董事长王拴红于1993年2月创立，是中国最早的期货公司之一。经过多年的发展，格林集团由初创时期注册资金100万元的公司已发展成为涉足期货、房产、保险三大领域的大型金融集团。
东岳庙坐落于北京朝阳门外大街中段，占地约6万平方米，初建于元代延祐六年（公元1319年），由中路及东西院组成，共七进，集廊院、四合院为一体，具有元、明、清三代建筑风格，距今有600多年的历史。东岳庙素以神像多、楹联多、碑刻多著称。图片为东岳庙我去过这个地方在朝阳区神路街。里面有东岳殿、官职司，行云布雨司、阜财殿、文财神比干为商朝老臣，为了直言上谏殷纣王，被小人费仲尤浑陷害，说妲己是妖孽迷惑纣王，毁了成汤八百年的社稷基业，比干作为丞相元老被挖了七窍玲珑心。众臣子对纣王很不满。都纷纷起了逆反之心。
《判我有罪》（Sentence Me Guilty）是由中国女性编剧及导演孙亮执导，李昕芸、吴镇宇、戴立忍、田小洁、李至正联袂主演的犯罪悬疑电影，于2016年5月6日在中国上映。该片根据真实案件改编，讲述了医院发生了一起惨烈的坠楼命案，由此牵出一场围绕金钱与欲望的黑幕，该影片入围了北京国际电影节“注目未来”单元。
Here地图是由诺基亚推出的地图服务。该款软件的功能是提供免费turn-by-turn语音导航，公共交通信息，以及丰富的道路交通信息等。但是也存在缺陷，比如在公共汽车以及地铁等重要公共交通信息提供上经常性的设置一些无意义的导航。
华南师范大学附属小学创建于1937年8月，原名勷勤大学教育学院附属小学，后几度易名为“广东省立文理学院附属小学”、“广东省文理学院附属小学”、“华南师范学院附属小学”、“山鹰小学”等，1982年10月定名为华南师范大学附属小学。学校于1995年晋升广东省一级学校行列，是全省唯一一所直属广东省教育厅和华南师范大学双重领导下的省一级学校。
玉蜀黍（学名：Zea mays L）是禾本科、玉蜀黍属植物，俗称玉米。 一年生高大草本。秆直立，通常不分枝，高1-4米，基部各节具气生支柱根。叶鞘具横脉；叶舌膜质，长约2毫米；叶片扁平宽大，线状披针形，基部圆形呈耳状。顶生雄性圆锥花序大型，主轴与总状花序轴及其腋间均被细柔毛；雄性小穗孪生，长达1厘米，小穗柄一长一短。颖果球形或扁球形，成熟后露出颖片和稃片之外，其大小随生长条件不同产生差异，一般长5-10毫米，宽略过于其长，胚长为颖果的1/2-2/3。花果期秋季。
