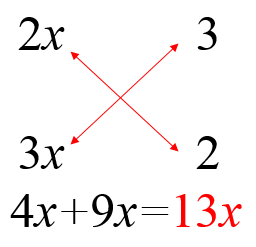基本概念

定义

把一个多项式在一个范围化为几个整式的积的形式，这种式子变形叫做这个多项式的因式分解，也叫作把这个多项式分解因式。

因式分解是中学数学中最重要的恒等变形之一，它被广泛地应用于初等数学之中，在数学求根作图、解一元二次方程方面也有很广泛的应用，是解决许多数学问题的有力工具。

因式分解方法灵活，技巧性强。学习这些方法与技巧，不仅是掌握因式分解内容所需的，而且对于培养解题技能、发展思维能力都有着十分独特的作用。学习它，既可以复习整式的四则运算，又为学习分式打好基础；学好它，既可以培养学生的观察、思维发展性、运算能力，又可以提高综合分析和解决问题的能力[1]。

相关结论

基本结论：分解因式为整式乘法的逆过程。

高级结论：在高等代数上，因式分解有一些重要结论，在初等代数层面上证明很困难，但是理解很容易。

1）因式分解与解高次方程有密切的关系。对于一元一次方程和一元二次方程，初中已有相对固定和容易的方法。在数学上可以证明，对于一元三次方程和一元四次方程，也有固定的公式可以求解。只是因为公式过于复杂，在非专业领域没有介绍。对于分解因式，三次多项式和四次多项式也有固定的分解方法，只是比较复杂。对于五次以上的一般多项式，已经证明不能找到固定的因式分解法，五次以上的一元方程也没有固定解法。

2）所有的三次和三次以上的一元多项式在实数范围内都可以因式分解，所有的二次或二次以上的一元多项式在复数范围内都可以因式分解。这看起来或许有点不可思议。比如x⁴+1,这是一个一元四次多项式，看起来似乎不能因式分解。但是它的次数高于3，所以一定可以因式分解。也可以用待定系数法将其分解，只是分解出来的式子并不整洁。(这是因为，由代数基本定理可知n次一元多项式总是有n个根，也就是说，n次一元多项式总是可以分解为n个一次因式的乘积。并且还有一条定理：实系数多项式的虚数根两两共轭的，将每对共轭的虚数根对应的一次因式相乘，可以得到二次的实系数因式，从而这条结论也就成立了。)

3）因式分解虽然没有固定方法，但是求两个多项式的公因式却有固定方法。因式分解很多时候就是用来提公因式的。寻找公因式可以用辗转相除法来求得。标准的辗转相除技能对于中学生来说难度颇高，但是中学有时候要处理的多项式次数并不太高，所以反复利用多项式的除法也可以但比较笨，不过能有效地解决找公因式的问题。

4）因式分解是很困难的，初中所接触的只是因式分解很简单的一部分。

分解一般步骤

1、如果多项式的首项为负，应先提取负号；

这里的“负”，指“负号”。如果多项式的第一项是负的，一般要提出负号，使括号内第一项系数是正的。

2、如果多项式的各项含有公因式，那么先提取这个公因式，再进一步分解因式；

要注意：多项式的某个整项是公因式时，先提出这个公因式后，括号内切勿漏掉1；提公因式要一次性提干净，并使每一个括号内的多项式都不能再分解。

3、如果各项没有公因式，那么可尝试运用公式、十字相乘法来分解；

4、如果用上述方法不能分解，再尝试用分组、拆项、补项法来分解。

口诀：先提首项负号，再看有无公因式，后看能否套公式，十字相乘试一试，分组分解要合适。

原则

1、分解因式是多项式的恒等变形，要求等式左边必须是多项式。

2、分解因式的结果必须是以乘积的形式表示。

3、每个因式必须是整式，且每个因式的次数都必须低于原来多项式的次数。

4、结果最后只留下小括号，分解因式必须进行到每一个多项式因式都不能再分解为止；

5、结果的多项式首项一般为正。在一个公式内把其公因子抽出，即透过公式重组，然后再抽出公因子；

6、括号内的首项系数一般为正；

7、如有单项式和多项式相乘，应把单项式提到多项式前。如(b+c)a要写成a(b+c)；

8、考试时在没有说明化到实数时，一般只化到有理数就够了，有说明实数的话，一般就要化到实数。

口诀：首项有负常提负，各项有“公”先提“公”，某项提出莫漏1，括号里面分到“底”。

分解方法

因式分解主要有十字相乘法，待定系数法，双十字相乘法，对称多项式，轮换对称多项式法，余式定理法等方法，求根公因式分解没有普遍适用的方法，初中数学教材中主要介绍了提公因式法、运用公式法、分组分解法。而在竞赛上，又有拆项和添减项法式法，换元法，长除法，短除法，除法等。

提公因式法

如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法。

各项都含有的公共的因式叫做这个多项式各项的公因式。公因式可以是单项式，也可以是多项式。

具体方法：在确定公因式前，应从系数和因式两个方面考虑。当各项系数都是整数时，公因式的系数应取各项系数的最大公约数字母取各项的相同的字母，而且各字母的指数取次数最低的。当各项的系数有分数时，公因式系数为各分数的最大公约数。如果多项式的第一项为负，要提出负号，使括号内的第一项的系数成为正数。提出负号时，多项式的各项都要变号。

基本步骤：

(1)找出公因式；

(2)提公因式并确定另一个因式；

①找公因式可按照确定公因式的方法先确定系数再确定字母；

②提公因式并确定另一个因式，注意要确定另一个因式，可用原多项式除以公因式，所得的商即是提公因式后剩下的一个因式，也可用公因式分别除去原多项式的每一项，求的剩下的另一个因式；

③提完公因式后，另一因式的项数与原多项式的项数相同。

口诀：找准公因式，一次要提尽，全家都搬走，留1把家守，提负要变号，变形看奇偶。

例：

注意：把变成不叫提公因式，因为括号内不得用分数。

公式法

如果把乘法公式的等号两边互换位置，就可以得到用于分解因式的公式，用来把某些具有特殊形式的多项式分解因式，这种分解因式的方法叫做公式法。

分解公式：

1、平方差公式：

即两个数的平方差，等于这两个数的和与这两个数的差的积。

2、完全平方公式：

即两个数的平方和加上(或减去)这两个数的积的2倍，等于这两个数的和(或差)的平方。

注意：能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数(或式)的平方和的形式，另一项是这两个数(或式)的积的2倍。

口诀：首平方，尾平方，积的二倍放中央。同号加、异号减，符号添在异号前。

推广：

(1)即三数和的平方，等于这三个数的平方和加上每两项的积的2倍。

(2)即四数和的平方，等于这四个数的平方和加上每两数的积的2倍。

即几个数的和的平方，等于这几个数的平方和加上每两数的积的2倍。

(3)

(4)

3、立方和公式：

即两数之和，乘它们的平方和与它们的积的差，等于这两个数的立方和。

推广：三项立方和公式：

即三数之和，乘它们的平方和与它们两两的积的差，等于这三个数的立方和减三数之积的三倍

变形：

4、立方差公式：

即两数之差，乘它们的平方和与它们的积的和，等于这两个数的立方差。

变形：

5、完全立方公式：

即两数之和(差)的立方等于这两个数的立方和(差)与每一个数的平方乘以另一个数3倍的和(和与差)。

6、两根式：

十字相乘法

对于型的式子如果能分解为数的积，且有时(即a与b和是一次项的系数)，那么；或对于型的式子如果有，且有时，那么。这种分解因式的方法叫做十字相乘法。

注：与十字相乘法对应的还有双十字相乘法

具体方法：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项。

口诀：分二次项，分常数项，交叉相乘求和得一次项。(拆两头，凑中间)

特点：

(1)二次项系数是1；

(2)常数项是两个数的乘积；

(3)一次项系数是常数项的两因数的和。

基本步骤：

(1)把二次项系数和常数项分别分解因数;

(2)尝试十字图，使经过十字交叉线相乘后所得的数的和为一次项系数;

(3)确定合适的十字图并写出因式分解的结果;

(4)检验。

例1：把6x²+13x+6分解因式

解：

∴原式=(2x+3)(3x+2)

例2：把3m³-3m²-60m分解因式

解：

∴原式=3m(m²-m-20)

=3m(m-5)(m+4)

双十字相乘法

对于某些二元二次六项式(x、y为未知数，其余都是常数)，用两次十字相乘法分解因式，这种分解因式的方法叫做双十字相乘法。

步骤：

(1)用十字相乘法分解二次项，得到一个十字相乘图(有两列)；

(2)把常数项f分解成两个因式填在第三列上，要求第二、第三列构成的十字交叉之积的和等于原式中的ey，第一、第三列构成的十字交叉之积的和等于原式中的dx．

(3)先以一个字母的一次系数分数常数项；

(4)再按另一个字母的一次系数进行检验；

(5)横向相加，纵向相乘。

例：分解因式：x²+5xy+6y²+8x+18y+12．

解析：这是一个二次六项式，可考虑使用双十字相乘法进行因式分解。

解:

x2y2

x3y6

∴原式=(x+2y+2)(x+3y+6)

轮换对称法

当题目为一个轮换对称式时，可用轮换对称法进行分解。

步骤：

（1）试根

把下列5个等式分别带入原式，找出令原式等于0的那个等式。

1、 x=0

2、 x=y

3、 x=-y

4、 x=y+z

5、 x=-y-z

（2）轮换

1、若x=0使原式=0 原式必有因式xyz

2、若x=y使原式=0 原式必有因式（x-y）（y-z）（z-x）

3、若x=-y使原式=0 原式必有因式（x+y）（y+z）（z+x）

4、若x=y+z使原式=0 原式必有因式（x-y-z）（y-z-x）（z-x-y）

5、若x=-y-z使原式=0 原式必有因式（x+y+z）

（3）对比次数

用原式的次数减去必有因式的次数，然后再乘上差的次数的对应的式子。（差几次添几次）

须添上的轮换对称式：

1次：x+y+z

2次：x²+y²+z²、xy+yz+zx

3次：x³+y³+z³、x²y+y²z+z²x、xy²+yz²+zx²、xyz

（4）根据次数待定系数

在需要乘上的式子前加上字母，待定系数。

（5）算出待定的系数

用特值法及恒等式性质算出待定的系数。

（6）得出答案

进行检验，写出答案。

例：分解因式：x²（y-z）³+y²（z-x）³+z²（x-y）³

解：x=y原式=0

必有因式（x-y）（y-z）（z-x）

原式为五次式，（x-y）（y-z）（z-x）为三次式，则需要补上二次式

设补上a（x²+y²+z²）+b（xy+yz+zx）

原式=（x-y）（y-z）（z-x）[a（x²+y²+z²）+b（xy+yz+zx）]

特值法：

令x=1 y=2 z=3

x²（y-z）³+y²（z-x）³+z²（x-y）³=（x-y）（y-z）（z-x）[a（x²+y²+z²）+b（xy+yz+zx）]

-1+32-9=（-1）·（-1）·2·（14a+11b）

22=28a+22b

14a+11b=11

令x=3 y=2 z=4

x²（y-z）³+y²（z-x）³+z²（x-y）³=（x-y）（y-z）（z-x）[a（x²+y²+z²）+b（xy+yz+zx）]

-72+4+16=1·（-2）·1·（29a+26b）

-52=-58a-52b

29a+26b=26

解得a=0

b=1

原式=（x-y）（y-z）（z-x）（xy+yz+zx）

分组分解法

通过分组分解的方式来分解提公因式法和公式分解法无法直接分解的因式，这种分解因式的方法叫做分组分解法。能分组分解的多项式有四项或大于四项，一般的分组分解有两种形式：二二分法，三一分法。

例1：因式分解ax+ay+bx+by

解析：把ax和ay分一组，bx和by分一组，利用乘法分配律，两两相配，立即解除了困难。

解：ax+ay+bx+by

=a(x+y)+b(x+y)

=(a+b)(x+y)

或

ax+ay+bx+by

=x(a+b)+y(a+b)

=(a+b)(x+y)

例2：因式分解5ax+5bx+3ay+3by

解析：系数不一样一样可以做分组分解，和上面一样，把5ax和5bx看成整体，把3ay和3by看成一个整体，利用乘法分配律轻松解出。

解：5ax+5bx+3ay+3by

=5x(a+b)+3y(a+b)

=(5x+3y)(a+b)

例3：因式分解x²-x-y²-y

解析：利用二二分法，再利用公式法a²-b²=(a+b)(a-b)，然后相合解决。

解：x²-x-y²-y

=(x²-y²)-(x+y)

=(x+y)(x-y)-(x+y)

=(x+y)(x-y-1)

例4：因式分解a²-b²-2bc-c²

解：a²-b²-2bc-c²

=a²-(b+c)²

=(a-b-c)(a+b+c)

拆添项法

把多项式的某一项拆开或填补上互为相反数的两项(或几项)，使原式适合于提公因式法、运用公式法或分组分解法进行分解,这种分解因式的方法叫做拆项补项法。要注意，必须在与原多项式相等的原则下进行变形。

例:分解因式：x³-9x+8．

分析：本题解法很多，这里只介绍运用拆项、添项法分解的几种解法，注意一下拆项、添项的目的与技巧．

解法1：将常数项8拆成-1+9．

原式=x³-9x-1+9

=(x³-1)-9x+9

=(x-1)(x²+x+1)-9(x-1)

=(x-1)(x²+x-8)

解法2将一次项-9x拆成-x-8x．

原式=x³-x-8x+8

=(x³-x)+(-8x+8)

=x(x+1)(x-1)-8(x-1)

=(x-1)(x²+x-8)

解法3将三次项x³拆成9x³-8x³．

原式=9x³-8x³-9x+8

=(9x³-9x)+(-8x³+8)

=9x(x+1)(x-1)-8(x-1)(x²+x+1)

=(x-1)(x²+x-8)

解法4 添加两项-x²+x²．

原式=x³-9x+8

=x³-x²+x²-9x+8

=x²(x-1)+(x-8)(x-1)

=(x-1)(x²+x-8)

配方法

对于某些不能利用公式法的多项式，可以将其配成一个完全平方式，然后再利用平方差公式，就能将其因式分解，这种分解因式的方法叫做配方法。属于拆项、补项法的一种特殊情况。也要注意必须在与原多项式相等的原则下进行变形。

例：分解因式x²+3x-40

解：x²+3x-40

=x²+3x+2.25-42.25

=(x+1.5)²-(6.5)²

=(x+8)(x-5)．

因式定理法

根据因式定理，用求多项式的根来确定多项式的一次因式，从而对多项式进行因式分解的方法叫做因式定理法。

具体方法：根据因式定理若是一元多项式的根，即成立，则多项式有一个因式，找出一元多项式的一次因式的关键是求多项式的根．对于任意多项式，要求出它的根是没有一般方法的，然而当多项式f(x)的系数都是整数时，即整系数多项式时，若既约分数q/p是整系数多项式的根，则必有是的约数，是的约数。特别地，当时，整系数多项式的整数根均为的约数。

注意：

(1)对于系数全部是整数的多项式，若(p,q为互质整数时)该多项式值为零，则q为常数项约数，p最高次项系数约数；

(2)对于多项式，为最高次项系数，为常数项，则有为约数。

例：f(x)=x²+5x+6，f(-2)=0，则可确定x+2是x²+5x+6的一个因式。(事实上，x²+5x+6=(x+2)(x+3)．)

换元法

选择多项式中的相同的部分换成另一个未知数，然后进行因式分解，最后再转换回来，这种分解因式的方法叫做换元法。注意，换元后勿忘还元。

例：分解因式(x²+x+1)(x²+x+2)-12

解：令y=x²+x,则

原式=(y+1)(y+2)-12

=y²+3y+2-12=y²+3y-10

=(y+5)(y-2)

=(x²+x+5)(x²+x-2)

=(x²+x+5)(x+2)(x-1)．

综合除法

令多项式，求出其根为，则该多项式可分解为。这种分解因式的方法叫做综合除法。

例：分解因式2x⁴+7x³-2x²-13x+6

解：令2x⁴+7x³-2x²-13x+6=0，

则通过综合除法可知，该方程的根为0.5，-3，-2，1．

所以2x⁴+7x³-2x²-13x+6=(2x-1)(x+3)(x+2)(x-1)．

令y=f(x)，做出函数y=f(x)的图象，找到函数图像与X轴的交点x1,x2,x3,……xn，则多项式可因式分解为f(x)=f(x)=a(x-x1)(x-x2)(x-x3)……(x-xn)．

主元法

在分解含多个字母的代数式时，选取其中一个字母为主元(未知数),将其它字母看成是常数，把代数式整理成关于主元的降幂排列(或升幂排列)的多项式，再尝试用公式法、配方法、分组分解法等分解因式的方法进行分解。这种分解因式的方法叫做主元法。

特殊值法

将2或10代入x，求出数p，将数p分解质因数，将质因数适当的组合，并将组合后的每一个因数写成2或10的和与差的形式，将2或10还原成x，即得因式分解式。这种分解因式的方法叫做特殊值法。

例：分解因式

解：令，则

将105分解成3个质因数的积，即

注意到多项式中最高项的系数为1，而3、5、7分别为，，，在时的值，

则可能等于，验证后的确如此。

待定系数法

在因式分解时，一些多项式经过分析，可以断定它能分解成某几个因式，但这几个因式中的某些系数尚未确定，这时可以用一些字母来表示待定的系数。由于该多项式等于这几个因式的乘积，根据多项式恒等的性质，两边对应项系数应该相等，或取多项式中原有字母的几个特殊值，列出关于待定系数的方程(或方程组)，解出待定字母系数的值，这种因式分解的方法叫作待定系数法。

例：分解因式

解析：这个多项式没有一次因式，因而只能分解为两个二次因式。

解：设

由此可得

a+c=-1

ac+b+d=-5

ad+bc=-6

bd=-4

解得a=1,b=1,c=-2,d=-4

则

二次多项式

根与系数关系二次多项式的因式分解

例：对于二次多项式，.

解：当时，设的解为

应用

多项式除以多项式

例：计算

解：原式=

多项式方程求根

例：在实数范围内解方程

解：

∴原方程即=0

又∵

∴在实数范围内，原方程等价于

∴在实数范围内，原方程的解为

解不等式及方程

例1：解不等式

解：原不等式可化为

则

或

∴

例2：解一元二次方程

解：整理得，

即，

∴

化简分式

例：化简

解：原式=

梅森合数分解

1、p=4r+3，如果8r+7也是素数，则：(8r+7)|(2P-1)。即(2p+1)|(2P-1)

例如：

23|(2¹¹-1)；11=4×2+3

47|(2²³-1)；23=4×5+3

167|(2⁸³-1)；83=4×20+3

2、p=2n×32+1,，则(6p+1)|(2P-1)，

例如：

223|(2³⁷-1)；37=2×2×3×3+1

439|(2⁷³-1)；73=2×2×2×3×3+1

3463|(2⁵⁷⁷-1)；577=2×2×2×2×2×2×3×3+1

3、p=2n×3m×5s-1,则(8p+1)|(2p-1)

例如；

233|(2²⁹-1)；29=2×3×5-1

1433|(2¹⁷⁹-1)；179=2×2×3×3×5-1

1913|(2²³⁹-1)；239=2×2×2×2×3×5-1

例题

例1：分解因式(1+y)²-2x²(1+y²)+x⁴(1-y)²．

解：原式=(1+y)²+2(1+y)x²(1-y)+x⁴(1-y)²-2(1+y)x²(1-y)-2x²(1+y²)(补项)

=[(1+y)+x²(1-y)]²-2(1+y)x²(1-y)-2x²(1+y²)(完全平方)

=[(1+y)+x²(1-y)]²-(2x)²

=[(1+y)+x²(1-y)+2x][(1+y)+x²(1-y)-2x]

=(x²-x²y+2x+y+1)(x²-x²y-2x+y+1)

=[(x+1)²-y(x²-1)][(x-1)²-y(x²-1)]

=[(x+1)²-y(x+1)(x-1)][(x-1)²-y(x+1)(x-1)]

=(x+1)(x+1-xy+y)(x-1)(x-1-xy-y)．

例2：求证：对于任何整数x,y，下式的值都不会为33：x⁵+3x⁴y-5x³y²-15x²y³+4xy⁴+12y⁵．

解：原式=(x⁵+3x⁴y)-(5x³y²+15x²y³)+(4xy⁴+12y⁵)

=x⁴(x+3y)-5x²y²(x+3y)+4y⁴(x+3y)

=(x+3y)(x⁴-5x²y²+4y⁴)

=(x+3y)(x²-4y²)(x²-y²)

=(x+3y)(x+y)(x-y)(x+2y)(x-2y)．

当y=0时，原式=x⁵不等于33；当y不等于0时，x+3y，x+y，x-y，x+2y，x-2y互不相同，而33不能分成四个以上不同因数的积，所以原命题成立。

例3：△ABC的三边a、b、c有如下关系式：-c²+a²+2ab-2bc=0，求证：这个三角形是等腰三角形。

分析：此题实质上是对关系式的等号左边的多项式进行因式分解。

证明：∵-c²+a²+2ab-2bc=0，

∴(a+c)(a-c)+2b(a-c)=0．

∴(a-c)(a+2b+c)=0．

∵a、b、c是△ABC的三条边，

∴a+2b+c>0．

∴a－c=0，

即a=c，△ABC为等腰三角形。

例4：把-12x2n×yn+18xn+2yn+1-6xn×yn-1分解因式。

解：-12x2n×yn+18xn+2yn+1-6xn×yn-1

=-6xn×yn-1(2xn×y-3x2y2+1)．